 Irrigation management affects the quality of winegrapes (Chapman et al. 2005). Achieving quality standards is essential for economic viability, and research conducted by the Commission’s Matthew Hoffman and his UC Davis colleagues found that winegrowers in Lodi, the Central Coast, and the Napa Valley, rank winegrape quality as their most important vineyard management goal (Hillis et al.2010, Hoffman et al. 2011 , Hoffman et al. 2011 ). Common irrigation management tools, like soil-based sensors, are excellent for providing data about available water in the soil. However, they fail to provide actionable information at the management scale of an entire field under one irrigation system. In other words, they are less user-friendly because the data they generate must be interpreted prior to making irrigation management decisions. In this Coffee Shop article my colleague Andrew McElrone and I write about a new UC Davis technology, called Surface Renewal, that measures the actual evapotranspiration (ET) of a crop field. Surface Renewal provides growers with irrigation management information that is simple, practical, and straight-forward.
Irrigation management affects the quality of winegrapes (Chapman et al. 2005). Achieving quality standards is essential for economic viability, and research conducted by the Commission’s Matthew Hoffman and his UC Davis colleagues found that winegrowers in Lodi, the Central Coast, and the Napa Valley, rank winegrape quality as their most important vineyard management goal (Hillis et al.2010, Hoffman et al. 2011 , Hoffman et al. 2011 ). Common irrigation management tools, like soil-based sensors, are excellent for providing data about available water in the soil. However, they fail to provide actionable information at the management scale of an entire field under one irrigation system. In other words, they are less user-friendly because the data they generate must be interpreted prior to making irrigation management decisions. In this Coffee Shop article my colleague Andrew McElrone and I write about a new UC Davis technology, called Surface Renewal, that measures the actual evapotranspiration (ET) of a crop field. Surface Renewal provides growers with irrigation management information that is simple, practical, and straight-forward.
Surface Renewal is an advancement from similar technologoes in that it estimates ET for an entire vineyard (as opposed to one plant) and for your specific vineyard (as opposed to a test case). Our research group, Drs. Andrew McElrone, Kyaw Tha Paw U, Rick Snyder, and I developed Surface Renewal in the Departments of Viticulture & Enology and Atmospheric Science (Shapland et al. 2012).Like the lysimeter at the UC Kearney Agricultural Center, Surface Renewal measures the actual water use by the vines and water loss from plant and soil surfaces to the atmosphere. Surface Renewal is different in that it measures ET over a broad area such as an entire vineyard, not just a single plant. Unlike California Irrigation Management Information System (CIMIS) Reference ET, which estimates the ET from a well-watered grass field somewhere down the road from your vineyard, Surface Renewal measures the actual amount of water that has evaporated from your specific vineyard.
The Surface Renewal system looks like a typical vineyard weather station. Unlike a weather station, which provides inferential information about an irrigation decision (i.e., it was hot yesterday), Surface Renewal informs the winegrower of the actual evaporative losses from a vineyard block. If you know how much water has evaporated from your vineyard, then you know how much water to replace with irrigation. Our intent is to provide winegrowers with a tool that quantifies the amount of water that evaporates from a vineyard block and the level of stress the vines are experiencing, and translates to the management decision of how long to turn on the irrigation pump.
Brief Theoretical Background to Surface Renewal
Surface Renewal measures how much water vapor the wind carries away from a crop. More specifically, it is a field-based sensor system that accounts for the energy and mass budget of individual eddies of wind that ephemerally come in contact with plant canopies. As the wind moves across a vineyard, water vapor is transferred from the vineyard into eddies of the wind. When an eddy of wind reaches our sensor in the vineyard, it informs us of the water vapor transfer over the area that the eddy has traveled.
For most vineyard conditions, Surface Renewal measures the ET over an approximately five acre area. If the vineyard is forty acres and the soil is uniform, the five acre area measured by Surface Renewal may be consistent with a broader area of the block. If the soils are not uniform, more than one Surface Renewal system may be required to characterize the ET of the entire vineyard block.
Quantifying Vineyard Actual ET, Managing Vine Stress and Estimating Pump Run-Time
The Surface Renewal ET data is sent to the grower as an email report with three tables. A PDF attachment with the same tables and additional figures, as well as a link to an interactive website, are also delivered in the email (For an example, click HERE). In this article we will focus on the three tables in the email body. The first email table has the recent and forecast Reference ET (see Table 1 below). The second table has the recent Actual ET from the vineyard, as well as how the Actual ET from the vineyard compares to the Reference ET (see Table 2 below). On the third table the grower can look up pump run-times based on when the last irrigation event occurred and what percent of Reference ET he or she wants to replace to the field (see Table 3 below).
It is important to understand the difference between Actual ET and Reference ET. Three factors primarily influence Actual ET:
- evaporative demand of the atmosphere,
- the amount of transpirational area of the crop, which is affected by vine spacing, trellis type, etc., and
- the availability of water in the soil to the vine.
The Actual ET from the vineyard, measured using Surface Renewal, is the gallons of water per vine that evaporated from the vineyard. Surface Renewal measures ET in acre-inches (an acre-inch of water is the amount of water needed to cover a one acre area to a depth of one inch), but the inches are converted to gallons of water per vine based on the vine spacing (for example, 6 feet by 11 feet). Assuming the canopy size has not changed much since the previous irrigation, a decrease in Actual ET may be due to either a decrease in evaporative demand or a decrease in water availability. By examining the previous week of Reference ET and the upcoming week of Reference ET, the grower can anticipate how weather variability may influence vineyard irrigation requirements.
We account for changes in evaporative demand by looking at the ratio of Actual ET over the Reference ET. If both the Actual ET and the Reference ET decrease, it is because there was a decrease in evaporative demand. In this case, the ratio of Actual ET over Reference ET does not change. If the Actual ET decreases but the Reference ET does not decrease, it is because the vines are running out of water. We would then see the ratio of Actual ET over Reference ET decrease.
__________________________________________________________________________________
Table 1. Reference ET: The Reference ET describes the water loss from a fully-irrigated grass field. To make the data more relevant to viticulture, the Reference ET is expressed in units of gallons per vine rather units of inches. This table tells the grower how evaporative demand is expected to change over the next week compared to the previous week.
| Last Week (gal per vine) | Yesterday (gal per vine) | Today (gal per vine) | Next Week (gal per vine) |
| 53.7 | 7.8 | 7.3 | 44.9 |
__________________________________________________________________________________
Table 2. Actual ET: The Actual ET from the vineyard measured using Surface Renewal and the ratio of Actual ET to Reference ET. The Actual ET tells the grower how much water has evaporated from the vineyard. The ratio of the Actual ET over the Reference ET tells the grower if a decrease in Actual ET is due to changes in evaporative demand or soil water availability.
| Site | Last Week Actual ET (gal per vine) |
Yesterday Actual ET (gal per vine) |
Last Week Actual ET/ Reference ET (unitless) |
Yesterday Actual ET/ Reference ET (unitless) |
| Block 36 | 39.8 | 6.2 | 0.74 | 0.79 |
__________________________________________________________________________________
Table 3. Pump Run-Time (hours): Irrigation pump run-time hours based on how many days have passed since the previous irrigation and the target percent of Reference ET for the application amount.
| Days Since Last Irrigation | Percentage of Reference ET | ||||||||||
| — 1 2 3 4 5 6 7 |
20% 1 3 4 5 6 8 9 |
30% 2 4 6 8 10 11 13 |
40% 3 5 8 10 13 15 18 |
50% 3 7 10 13 16 19 22 |
60% 6 8 12 15 19 23 27 |
70% 5 9 14 18 22 27 31 |
80% 5 11 16 20 26 30 36 |
90% 6 12 18 23 29 34 40 |
100% 8 13 20 26 32 38 45 |
110% 7 15 21 28 35 42 49 |
120% 9 16 23 31 38 46 53 |
__________________________________________________________________________________
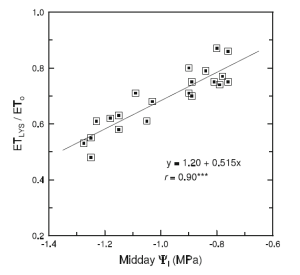
Figure 2. The ratio of Actual ET over Reference ET (ETLYS / ETo) as a function of midday leaf water potential (Midday Ψl) from Williams et al. 2012. The authors of the article measured Actual ET using a lysimeter. As we move from right to left on the x-axis, the midday leaf water potential decreases and the vines become more water stressed. As the vines become more stressed, the ratio of Actual ET decreases relative to the Reference ET. By giving the winegrower the ratio of Actual ET to Reference ET, Surface Renewal allows the winegrower to manage vine stress.
You may have noticed we are not using crop coefficients. It is time-consuming and difficult to accurately estimate the crop coefficient for a particular vineyard. In our experiences, if the crop coefficient estimation is off the mark, it makes the interpretation of the Actual ET data very difficult. We have decided it is better to use simply the Reference ET to contextualize the Actual ET values.
If you know how much water has evaporated from your vineyard, then you know how much water to replace with an irrigation event. Let’s say the vineyard Actual ET has been 80% of the Reference ET. If the winegrower decides to keep the vineyard at the current stress level of Actual ET over Reference ET equal to 80%, he or she looks up 80% under “Percentage of Reference ET”. The pump run-time can be found where the 80% column meets the horizontal row for the number of days since the previous irrigation event.
Irrigation decisions are nuanced and site specific. No technology can replace the lifetime of viticultural experience required with a particular block to get the irrigation decision right. The winegrower can weigh the Reference ET, the Actual ET, and the pump run-times against his or her experiences, and find peace of mind that his or her irrigation management strategy is proceeding as expected.
Conclusion
Surface Renewal has three advantages over soil- or single plant-based sensor approaches:
- it provides the ET from your vineyard rather than an estimate of ET from well-watered grass,
- it measures over a broad area, and
- the data translates directly to a management decision.
Our research group is working on improving the usability and applicability of Surface Renewal for winegrowers like you. If you have questions or comments, please send me an email at tmshapland@ucdavis.edu.


